暂无测试数据。

U538275 麻将扑克(poke)

题目背景

欢迎来到麻州扑克的世界！这里充满了刺激和机遇，准备好迎接挑战了吗？

在麻州扑克中，我们使用了一副特殊的扑克牌。牌堆包含了点数1到9的条纹牌，分别有$a_1,a_2,\ldots,a_9$张；同时也包含了点数为1到9的圆筒牌，分别有$b_1,b_2,\ldots,b_9$张。一共有$\sum_{i = 1}^{9}a_i+\sum_{i = 1}^{9}b_i$张牌（保证$\sum_{i = 1}^{9}a_i+\sum_{i = 1}^{9}b_i\geq7$），下图是圆筒牌（第一行）和条纹牌（第二行）的样式示意图。 上图1：圆筒牌和条纹牌样式示意图

游戏规则如下：每局游戏开始时，庄家会先从一对、两对、三条、顺子、葫芦、四张、同花顺这七种牌型中选择一种作为目标牌型，接着庄家首先从牌堆中抽取五张牌作为庄家的手牌，而你将继续从牌堆中抽取两张牌作为你的手牌。你需要在庄家手牌的五张牌中选取三张牌（第一行）和你的两张牌（第二行）组合成你最终的牌型，下图是选取最终牌型的示意图。

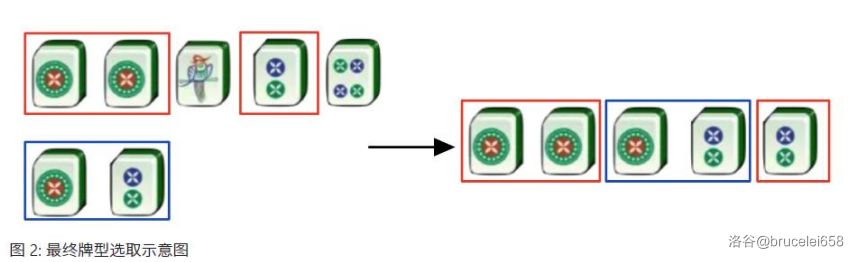
如果你最终牌型与庄家开局时选择的目标牌型完全一致，则恭喜你获得胜利，将会获得巨额奖励！但是如果你的最终牌型与庄家开局选择的牌型不一致，则很遗憾你输了，将会面临严峻的惩罚。现在你非常想获得胜利，你的任务是计算给定庄家选择的目标牌型的情况下，你绝对聪明时获胜概率是多少。

以下是不同牌型的详细定义：

题目描述

无

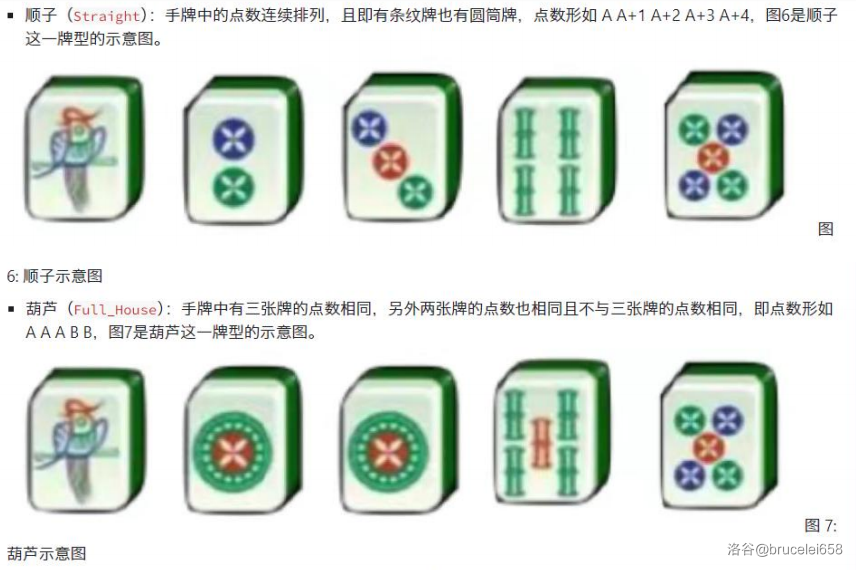
输入格式

第一行包含九个整数$a_1,a_2,\ldots,a_9$，表示点数1到9的条纹牌的数量。 第二行包含九个整数$b_1,b_2,\ldots,b_9$，表示点数1到9的圆筒牌的数量。 第三行为一个字符串{Pair, Two_Pairs, Three_of_a_Kind, Straight, Full_House, Four_of_a_Kind, Straight_Flush}，表示庄家开局时选择的目标牌型。

输出格式

输出共1行，如果你绝对聪明时获胜的概率为最简分数$\frac{x}{y}$，则需要输出$x \cdot y^{-1} \mod\ 998244353$，其中$y^{-1}$表示$y$在模998244353意义下的逆元。

输入输出样例 #1

输入 #1

5 2 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
Four_of_a_Kind

输出 #1

380283564

说明/提示

【样例1解释】

在本局中，你绝对聪明时获胜的可能为 $\frac{20}{21}$。

【数据范围】

对于30%的数据，满足 $\sum_{i = 1}^{9}a_i+\sum_{i = 1}^{9}b_i \leq 15$。 对于另外30%的数据，满足至多只有6种牌的数量不为0。 对于100%的数据，满足 $\sum_{i = 1}^{9}a_i+\sum_{i = 1}^{9}b_i \leq 10^{5}$。

【提示】

逆元的相关知识：设$y^{-1}$表示$y$在模998244353意义下的逆元，则有$y \cdot y^{-1} \equiv 1(\text{mod }998244353)$。 逆元的一种求解方法：由于998244353是质数，当$y$不是998244353的倍数时，可以由费马小定理有$y^{-1} \equiv y^{(998244353 - 2)}(\text{mod }998244353)$。