#U2021OG3. Permutation
Permutation
Bessie 在二维平面上有 N(3≤N≤40)个最爱的不同的点,其中任意三点均不共线。对于每一个 1≤i≤N,第 i 个点可以用两个整数 x 和 y 表示(0≤x,y≤10)。Bessie 按如下方式在这些点之间画一些线段:
- 她选择这N 个点的某个排列 p,p,…,p。
- 她在点 p 和 p、p 和 p、p 和 p 之间画上线段。
- 然后依次对于从 4 到 N 的每个整数 i,对于所有 j<i,她从 p到 p 画上一条线段,只要这条线段不与任何已经画上的线段相交(端点位置相交除外)。
Bessie 注意到对于每一个 i,她都画上了恰好三条新的线段。计算 Bessie 在第 1 步可以选择的满足上述性质的排列的数量,结果对 10+7 取模。
输入格式(从终端 / 标准输入读入):
输入的第一行包含 N。以下 N 行,每行包含两个空格分隔的整数 x 和 y。
输出格式(输出至终端 / 标准输出):
输出排列的数量模 10+7 的结果。
输入样例:
4
0 0
0 4
1 1
1 2
输出样例:
0
没有排列满足该性质。
输入样例:
4
0 0
0 4
4 0
1 1
输出样例:
24
所有排列均满足该性质。
输入样例:
5
0 0
0 4
4 0
1 1
1 2
输出样例:
96
一个满足该性质的排列为 (0,0),(0,4),(4,0),(1,2),(1,1)。对于这个排列,
- 首先,她在 (0,0),(0,4) 和 (4,0) 两两之间画上线段。
- 然后她从 (1,2) 向 (0,0),(0,4) 和 (4,0) 画上线段。
- 最后,她从 (1,1) 向 (1,2),(4,0) 和 (0,0) 画上线段。
如图:
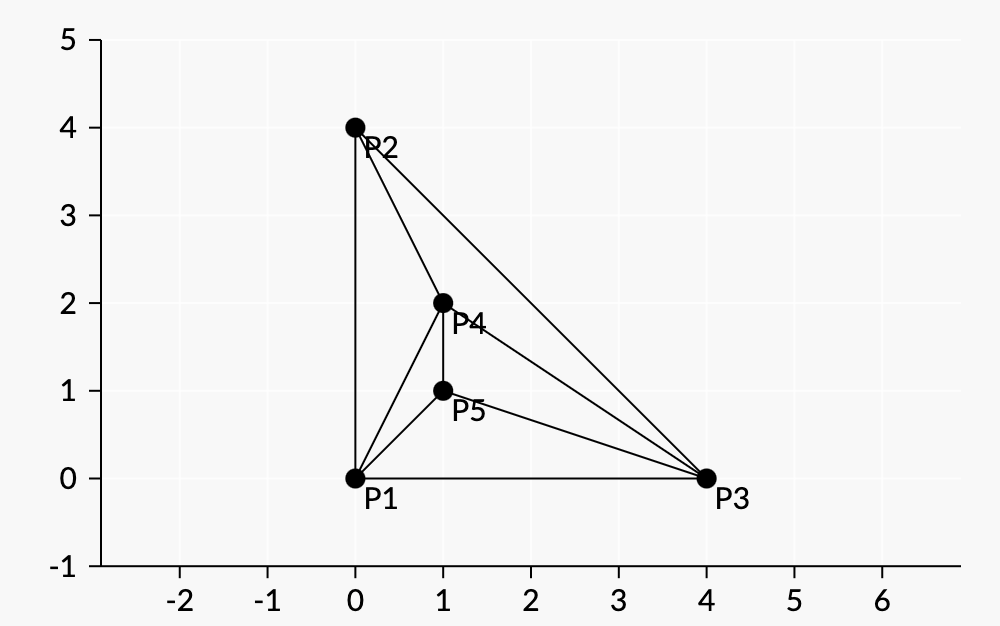
如果排列的前四个点是 (0,0)、(1,1)、(1,2) 和 (0,4) 以某种顺序排列,则此排列不满足该性质。
测试点性质:
- 测试点 1-6 满足 N≤8。
- 测试点 7-20 没有额外限制。
